(4.1) Combinatorics

There is enumerating the number of different possible combinations, and then there is the probability of a given combination.

Do in order of: 3 types of permutations 3 types of combinations binomial inclusion exclusion derangements

What do you mean by derangements in combinatorial mathematics?

The number of rearrangements, if n things are arranged in a row, such that none of them will occupy their original positions, are called derangements.

Give the formula for the number of derangements of n distinct things.

Dn = n![1 – (1/1!) + (1/2!) – (1/3!) + …. + (-1)n(1/n!)] where n≥2. Here, Dn is the number of derangements of n distinct things.

Give the Principle of Inclusion and Exclusion formula.

The Principle of Inclusion and Exclusion formula is given by n(A⋃B) = n(A) + n(B) – n(A⋂B).

What do you mean by the cardinality of a set?

The cardinality of a set is the number of elements in a set. Let A = {1, 2, 3, 6}. The cardinality of set A = 4.

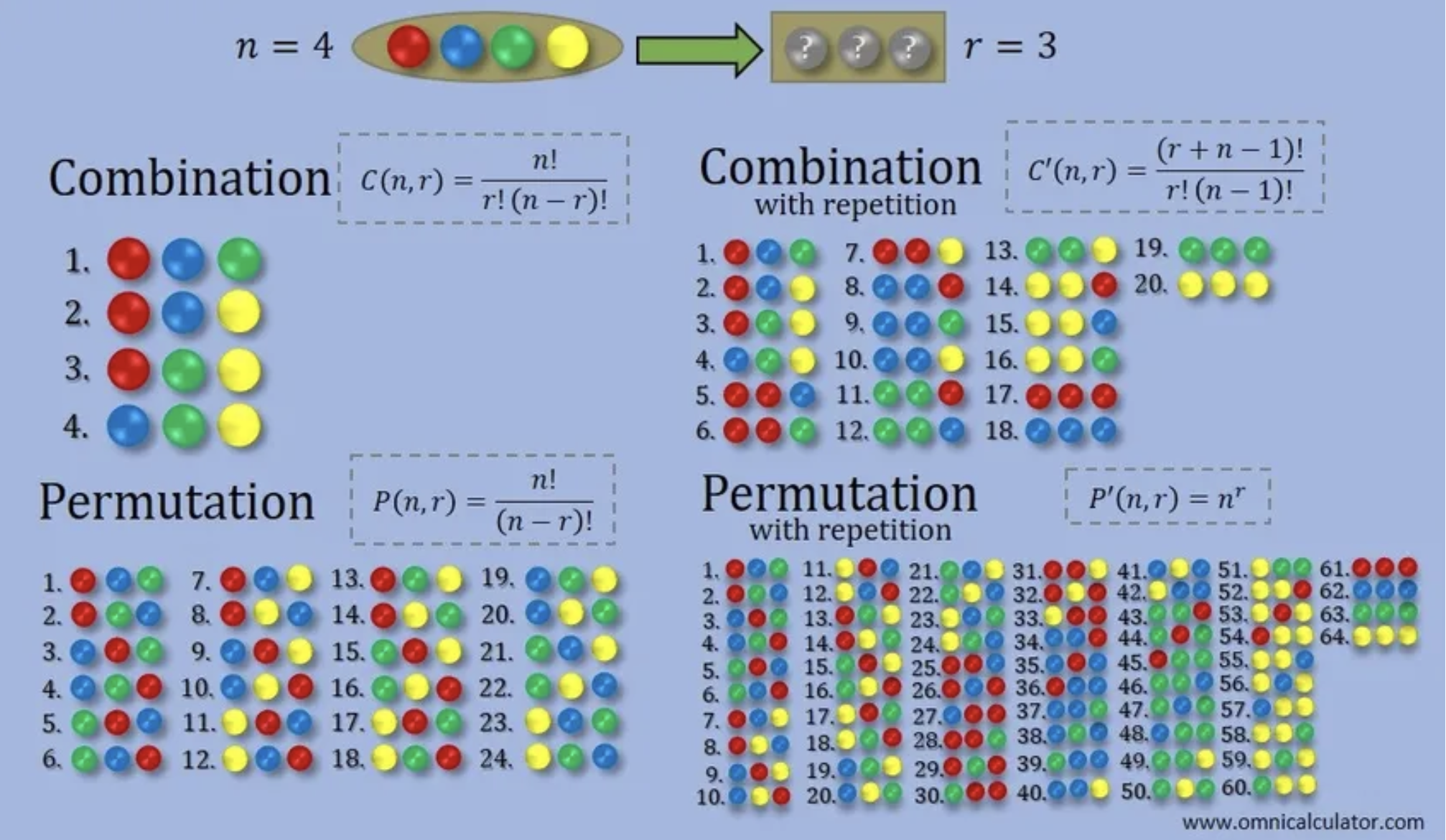
How many different ways can you order 5 rocks?

Permutation

This is how a permutation arises. In a permutation, the order of elements matters, and membership is fixed.

5! = 5 \times 4 \times 3 \times 2 \times 1 = 120

How many different orderings of 3 items can you choose from 5 (order matters)?

⚘ This is also a permutation, but a more general case.

Use $no. permutations = \frac{n !}{( n - k )!}$ Where

$n =$ the total number of items
$k =$ the number of items being selected

↳ Great. Can you re-answer the first question using this formula? (How many different ways can you order 5 rocks)

☞ Use $n = 5, k = 5$

##### ↳ I have 2 blue balls, 3 green balls, and 4 red balls. How many different ways are there to order them such that each permutation has a unique sequence of colours (the balls are otherwise identical)

⚘ This is known as the number of permutations of a multiset (ordinary sets can only have one of each ‘type’, multisets are defined as in this question).

Total permutations = $\frac{( n )!}{n _{1} ! \times n _{2} ! \times \dots \times n _{k} !}$ Where $n$ is the total number of items in the multiset and $n_{1}, n_{2}, \dots, n_{k}$ are the numbers of identical items in each of the $k$ different categories within the multiset.

So there are $\frac{9 !}{2 ! \times 3 ! \times 4 !}$ different ways that the balls can be arranged.

How many different ways can you select 3 cars from 8?

⚘ This is how a combination arises. It involves the choose function, a handy formula which tells you the number of different ways you can select $k$ items from $n$ total items.

Combinations vs. Permutations

At this point, it’s very important to take a step back and consider the fundamental difference between combinations and permuations

Combinations: Used when the order of selection does not matter (different orderings of the same items are considered the same)

Permutations: Used when the order of selection does matter (different orderings of the same items are considered distinct)

For example, would you use a combination or permutation to answer the following question: ”In a class of 30 students, how many ways can a committee of 4 students be formed, and how many ways can you arrange 4 students in a line for a presentation?”

It should be obvious which one is appropriate to use, merely by asking ‘does the order matter?’

If you have 9 switches that can be either `on` or `off`, how many different combinations can you have?

⚘ This is a combination of binary choices. The formula is very intuitive.

☞ There are $9$ switches ☞ Each switch can either be on or off ( $2$ choices) ☞ $2 * 2 * 2 * \dots$ ☞ $2^{9}$ total combinations

Given 7 unique integers $[1, 2, 3, 4, 5, 6, 7]$ , how many distinct subsets can be formed? In other words, how large is the power set?

Same logic as the previous question. For a set with $n$ elements, the number of subsets (or the size of the power set) is $2^{n}$ .
This is because each element in the set has two choices: it can either be included in a subset or not.
Note that this includes the empty set $[]$ , which is the case when all elements opt of being included in a subset.

Bonus question: How could you code a function to return all possible subsets of a list such as `[1, 2, 3, 4, 5, 6, 7]`?

Input: nums = [1,2,3]
Output: [[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]]

Hint: think about how the formula for number of subsets, $2^{n}$ works, and how you could adapt it to generate subsets.

[[2.10 Backtracking#LC 78. [Subsets](https //leetcode.com/problems/subsets/)|See the answer here]].

How many ways can 4 people get their hats back such that no one gets their own hat?

⚘ This is a classic example of a derangement. These are permutations where no element appears in its original position.

The formula for the number of derangements of $n$ distinct items, denoted as $! n$ , is given by:

$! n = n! (\frac{1}{0 !} - \frac{1}{1 !} + \frac{1}{2 !} - \frac{1}{3 !} + ... + \frac{( - 1 ) ^{n}}{n !})$

For 4 people (or 4 hats), the formula becomes:

$! 4 = 4! (\frac{1}{0 !} - \frac{1}{1 !} + \frac{1}{2 !} - \frac{1}{3 !} + \frac{1}{4 !})$

The number of ways 4 people can get their hats back such that no one gets their own hat (a derangement) is exactly 9. This result is obtained by applying the formula for derangements to 4 items.

$6 + 3 = 9$ ways

↳ How many ways result in only 1 person getting their original hat back?

⚘ To answer this, we need to extend the formula for a derangement to this: $(k n) \cdot! (n - k)$

Let 1 person get their original hat back. The problem then becomes; how many different ways can the remaining 3 people recieve hats such that no one gets their original hat back.

In fact, no new formula is needed - you only need your n choose k and derangement. Think about it like this: first, choose the one lucky person who gets their hat back, and then, how many ways are there for remaining 3 people to get hats back that aren’t theirs. Since you can start with 4 different people…

↳ How many ways result in exactly 2 people getting their original hat back?

↳ How many ways result in exactly 3 people getting their original hat back?

If 3 people have their original hat, so must the 4th person. Therefore, there are 0 ways which result in this.

Derangment is only defined for $n \geq 2$

↳ How many ways result in all 4 people getting their original hat back?

There is clearly only 1 assignment in which they all get their respective hats back.

↳ Can you convert these all into probabilities?

They are all disjoint and mutually exclusive events, so simply divide by the total number of possible permutations/assignments, $4! = 24$ .

E.g $P r = \frac{9}{24}$

↳ Now imagine the general case of $n$ people and $n$ hats. What is the probability that any particular person gets their original hat back?

$1/ n$ - by symmetry, they have an equal probability of getting any one of the $n$ hats back, so there is a $1/ n$ chance that it is their original one.

☞ How do you know the apply symmetry? Well, would there be any reason for it to be more or less likely to receive any specific hat? No. ∴ There must be uniform probability of receiving any given hat.

↳ Use this fact, and linearity of expectation, in order to calculate the expected number of people who get their original hat back, out of $n$ people.

☞ First, let $X_{i}$ be the indicator random variable that person $i$ gets their original hat back.

☞ I.e, if they got their original hat back, $X=1$, otherwise $X=0$.

☞ Then the total number of people who get their original hat back is $Y = X_{1} + \dots + X_{n}$

☞ Use linearity of expectation: $E (Y) = E (X_{1}) + \dots + E (X_{n})$ ∴ On average, only 1 person gets their hat back - no matter the value of $n$ .

How many ways can you distribute 10 books to 3 students so that the first student gets 5 books, the second student gets 3 books, and the third student gets 2 books?

⚘ An extension of the Combination Formula: The number of ways to choose k items from n items is given by $(k n)$ .

☞ For the first student, choose 5 books from 10: $(5 10)$ .

☞ For the second student, choose 3 books from the remaining 5: $(3 5)$ .

☞ The third student gets the remaining 2 books, which is a single combination: $(2 2)$ .

☞ Calculate the total ways by multiplying these combinations… ∴ Total ways = $(5 10) \times (3 5) \times (2 2) = 2520$

Thus, there are 2,520 different ways to distribute the books among the three students as per the given criteria.

↳ Translate this into a probability of this event occurring.

☞ To find the probability of this specific distribution happening by chance… Probability = $\frac{Favorable Outcomes}{Total Outcomes} = \frac{2520}{3 ^{10}}$

Q6) How many successes can I expect when drawing a sample without replacement from a population?

⚘ This is an application of the Hypergeometric Distribution

The hypergeometric distribution models the number of successes in a sample drawn without replacement from a population. Its PMF is: $P (X = k) = \frac{( k K ) ( n - k N - K )}{( n N )}$ Where:

( N ) is the total population size.
( K ) is the number of success states in the population.
( n ) is the number of draws.
Expected value (mean) = ( n \frac{K}{N} )
Variance = ( n \frac{K}{N} \frac{N-K}{N} \frac{N-n}{N-1} )

Q7) If I choose $5$ cards from a deck of $52$ cards (without replacement), what is the probability that $x = 3$ of them are red?

Hint: Hypergeometric Distribution

Answer: $P r (X = 3) \approx 0.325$

⊛

Let’s get distribution-ey

☞ The hypergeometric distribution deals with the distribution of the number of successes and failures when drawing from a finite population without replacement

Hypergeometric Distribution Parameters:

$N$ : Total number of items in the population.
$K$ : Total number of success items in the population.
$n$ : Number of items drawn without replacement
$k$ : Number of observed successes.

The probability of drawing exactly $k$ successes in $n$ draws from the population is given by: $P (X = k) = \frac{( k K ) ( n - k N - K )}{( n N )}$

Mean: $E (X) = n \frac{K}{N}$
Variance: $Va r (X) = n \frac{K}{N} \frac{N - K}{N} \frac{N - n}{N - 1}$

Explanation:

$(k K)$ : This gives us the number of ways to choose (k) successes from the (K) successes available in the population.
$(n - k N - K)$ : This represents the number of ways to choose the remaining $n - k$ failures from the $N - K$ failures in the population.
$(n N)$ : This is the total number of ways to choose any $n$ items from the $N$ items in the population.

The fraction $\frac{( k K ) ( n - k N - K )}{( n N )}$ computes the proportion of ways to get $k$ successes and $n - k$ failures out of all possible ways to draw $n$ items. This proportion gives the probability of observing exactly $k$ successes in $n$ draws.

The beauty of this formula is that it accounts for all possible combinations of successes and failures one might get when drawing from the population.

**Note that this is not the same thing as a Binomial Distribution with $n = 5, p = 0.5$ because you are sampling without replacement, instead of treating each card as an independent Bernoulli trial with constant probability of success.

Revisiting the question:

[write out the calculations labelling the logic]

(Q2) In the first round of a mario kart tournament, everyone must play every other person once. There are 5 people

5 choose 2?

Stats and Bars method

Selecting from a set with replacement, but order does not matter.

Let’s play poker. First question, how many possible 5-card poker hands exist?

↳ How many four-of-a-kind hands are there?

☞ There are $13$ different ‘ranks’ that the 4-of-a-kind could be.

☞ For each one, the last card can be any of the $48$ remaining cards.

☞ So, $13 * 48 = 624$

↳ How many hands represent a full house?

☞ In sequence, we need to choose the value of the triple, $13$ choices; the suits of the triple, $(3 4)$ choices.

☞ Then the value of the pair, $12$ choices; and the suits of the pair, $(2 4)$ choices.

☞ So the number of hands with a full house is $13 \times (3 4) \times 12 \times (2 4) = 13 \times 4 \times 12 \times 6 = 3, 744$ .

Note: when selecting the ranks of the triple and pair, why have we used a permutation ( $13 \times 12$ ) rather than a combination ( $(2 13)$ )? If you’re not sure, try this question. Answer: the ranks are not interchangeable; a 555 33 is a different hand to a 333 55

↳ How many two-pair hands are there?

The probability of receiving a particular hand, such as a Royal Flush, is independent of the number of players at the table, as long as there are enough cards for each player to receive a hand. This is because the probability calculation is based on your specific hand, which is randomly drawn from the deck, regardless of how many other hands are also being drawn.

$P r (Royal Flush ∣ Playing with 2 people) =$
$P r (Royal Flush ∣ Playing with 3 people) =$
$P r (Royal Flush ∣ Playing with 4 people)$

In the entire outcome space of possible poker hands, there are only $4$ royal flushes - one for each suit.

A♠K♠Q♠J♠10♠
A♥K♥Q♥J♥10♥
A♣K♣Q♣J♣10♣
A♦K♦Q♦J♦10♦

Hence,

P r (Royal Flush = \frac{4}{( 5 52 )})

↳ Under what three conditions is it okay to compute probabilities in this combinatoric way? E.g. $probability = \frac{no. outcomes in this event}{no. total outcomes}$

Every outcome is equally likely (every possible 5 card hand is equally likely)
Events are independent (applies when multiplying)
The sample must be randomly sampled (who’s dealing?)

Nice! and now you know how to calculate the probabilities of poker hands.

Find the number of ways that you can put 7 letters into their respective envelopes such that exactly 3 go into the right envelope.

Screwy pirates: Having peacefully divided the loot (in chapter 2), the pirate team goes on for more looting and expands the group to 11 pirates. To protect their hard-won treasure, they gather together to put all the loot in a safe. Still being a democratic bunch, they decide that only a majority - any majority - of them together can open the safe. So they ask a locksmith to put a certain number of locks on the safe. To access the treasure, every lock needs to be opened. Each lock can have multiple keys; but each key only opens one lock. The locksmith can give more than one key to each pirate. What is the smallest number of locks needed? And how many keys must each pirate carry?7

Two assertions

any 5 pirates must be missing one key
the other 6 pirates must have access to this one key

⚘ DSX.com

Explorer

(4.1) Combinatorics

What do you mean by derangements in combinatorial mathematics?

Give the formula for the number of derangements of n distinct things.

Give the Principle of Inclusion and Exclusion formula.

What do you mean by the cardinality of a set?

How many different ways can you order 5 rocks?

How many different orderings of 3 items can you choose from 5 (order matters)?

↳ Great. Can you re-answer the first question using this formula? (How many different ways can you order 5 rocks)

How many different ways can you select 3 cars from 8?

If you have 9 switches that can be either `on` or `off`, how many different combinations can you have?

Given 7 unique integers $[1, 2, 3, 4, 5, 6, 7]$ , how many distinct subsets can be formed? In other words, how large is the power set?

Bonus question: How could you code a function to return all possible subsets of a list such as `[1, 2, 3, 4, 5, 6, 7]`?

How many ways can 4 people get their hats back such that no one gets their own hat?

↳ How many ways result in only 1 person getting their original hat back?

↳ How many ways result in exactly 2 people getting their original hat back?

↳ How many ways result in exactly 3 people getting their original hat back?

↳ How many ways result in all 4 people getting their original hat back?

↳ Can you convert these all into probabilities?

↳ Now imagine the general case of $n$ people and $n$ hats. What is the probability that any particular person gets their original hat back?

↳ Use this fact, and linearity of expectation, in order to calculate the expected number of people who get their original hat back, out of $n$ people.

How many ways can you distribute 10 books to 3 students so that the first student gets 5 books, the second student gets 3 books, and the third student gets 2 books?

↳ Translate this into a probability of this event occurring.

Q6) How many successes can I expect when drawing a sample without replacement from a population?

Q7) If I choose $5$ cards from a deck of $52$ cards (without replacement), what is the probability that $x = 3$ of them are red?

Let’s get distribution-ey

(Q2) In the first round of a mario kart tournament, everyone must play every other person once. There are 5 people

Stats and Bars method

Let’s play poker. First question, how many possible 5-card poker hands exist?

↳ How many four-of-a-kind hands are there?

↳ How many hands represent a full house?

↳ How many two-pair hands are there?

↳ What is the chance you get a royal flush when playing with 4 others?

↳ Under what three conditions is it okay to compute probabilities in this combinatoric way? E.g. $probability = \frac{no. outcomes in this event}{no. total outcomes}$

Find the number of ways that you can put 7 letters into their respective envelopes such that exactly 3 go into the right envelope.

Graph View

Table of Contents

Backlinks

⚘ DSX.com

Explorer

(4.1) Combinatorics

What do you mean by derangements in combinatorial mathematics? §

Give the formula for the number of derangements of n distinct things. §

Give the Principle of Inclusion and Exclusion formula. §

What do you mean by the cardinality of a set? §

How many different ways can you order 5 rocks? §

How many different orderings of 3 items can you choose from 5 (order matters)? §

↳ Great. Can you re-answer the first question using this formula? (How many different ways can you order 5 rocks) §

How many different ways can you select 3 cars from 8? §

If you have 9 switches that can be either on or off, how many different combinations can you have? §

Given 7 unique integers [1,2,3,4,5,6,7], how many distinct subsets can be formed? In other words, how large is the power set? §

Bonus question: How could you code a function to return all possible subsets of a list such as [1, 2, 3, 4, 5, 6, 7]? §

How many ways can 4 people get their hats back such that no one gets their own hat? §

↳ How many ways result in only 1 person getting their original hat back? §

↳ How many ways result in exactly 2 people getting their original hat back? §

↳ How many ways result in exactly 3 people getting their original hat back? §

↳ How many ways result in all 4 people getting their original hat back? §

↳ Can you convert these all into probabilities? §

↳ Now imagine the general case of n people and n hats. What is the probability that any particular person gets their original hat back? §

↳ Use this fact, and linearity of expectation, in order to calculate the expected number of people who get their original hat back, out of n people. §

How many ways can you distribute 10 books to 3 students so that the first student gets 5 books, the second student gets 3 books, and the third student gets 2 books? §

↳ Translate this into a probability of this event occurring. §

Q6) How many successes can I expect when drawing a sample without replacement from a population? §

Q7) If I choose 5 cards from a deck of 52 cards (without replacement), what is the probability that x=3 of them are red? §

Let’s get distribution-ey §

(Q2) In the first round of a mario kart tournament, everyone must play every other person once. There are 5 people §

Stats and Bars method §

Let’s play poker. First question, how many possible 5-card poker hands exist? §

↳ How many four-of-a-kind hands are there? §

↳ How many hands represent a full house? §

↳ How many two-pair hands are there? §

↳ What is the chance you get a royal flush when playing with 4 others? §

↳ Under what three conditions is it okay to compute probabilities in this combinatoric way? E.g. probability=no. total outcomesno. outcomes in this event​ §

Find the number of ways that you can put 7 letters into their respective envelopes such that exactly 3 go into the right envelope. §

Graph View

Table of Contents

Backlinks

What do you mean by derangements in combinatorial mathematics?

Give the formula for the number of derangements of n distinct things.

Give the Principle of Inclusion and Exclusion formula.

What do you mean by the cardinality of a set?

How many different ways can you order 5 rocks?

How many different orderings of 3 items can you choose from 5 (order matters)?

↳ Great. Can you re-answer the first question using this formula? (How many different ways can you order 5 rocks)

How many different ways can you select 3 cars from 8?

If you have 9 switches that can be either `on` or `off`, how many different combinations can you have?

Given 7 unique integers $[1, 2, 3, 4, 5, 6, 7]$ , how many distinct subsets can be formed? In other words, how large is the power set?

Bonus question: How could you code a function to return all possible subsets of a list such as `[1, 2, 3, 4, 5, 6, 7]`?

How many ways can 4 people get their hats back such that no one gets their own hat?

↳ How many ways result in only 1 person getting their original hat back?

↳ How many ways result in exactly 2 people getting their original hat back?

↳ How many ways result in exactly 3 people getting their original hat back?

↳ How many ways result in all 4 people getting their original hat back?

↳ Can you convert these all into probabilities?

↳ Now imagine the general case of $n$ people and $n$ hats. What is the probability that any particular person gets their original hat back?

↳ Use this fact, and linearity of expectation, in order to calculate the expected number of people who get their original hat back, out of $n$ people.

How many ways can you distribute 10 books to 3 students so that the first student gets 5 books, the second student gets 3 books, and the third student gets 2 books?

↳ Translate this into a probability of this event occurring.

Q6) How many successes can I expect when drawing a sample without replacement from a population?

Q7) If I choose $5$ cards from a deck of $52$ cards (without replacement), what is the probability that $x = 3$ of them are red?

Let’s get distribution-ey

(Q2) In the first round of a mario kart tournament, everyone must play every other person once. There are 5 people

Stats and Bars method

Let’s play poker. First question, how many possible 5-card poker hands exist?

↳ How many four-of-a-kind hands are there?

↳ How many hands represent a full house?

↳ How many two-pair hands are there?

↳ What is the chance you get a royal flush when playing with 4 others?

↳ Under what three conditions is it okay to compute probabilities in this combinatoric way? E.g. $probability = \frac{no. outcomes in this event}{no. total outcomes}$

Find the number of ways that you can put 7 letters into their respective envelopes such that exactly 3 go into the right envelope.